如何在Python中打印帕斯卡三角形

本教程将教你如何在Python中为给定的行数打印帕斯卡三角形。

你将首先学习如何构造帕斯卡三角形。然后你将编写一个Python函数并学习进一步优化它。

▶️ 让我们开始吧！

什么是帕斯卡三角形及如何构造它？

打印给定行数的帕斯卡三角形是一个常见的面试问题。

在帕斯卡三角形中，第 i 行有 i 个元素。

所以第一行有一个元素，为1。而后续行中的每个元素都是其上方两个数字的和。

下图说明了如何构造五行帕斯卡三角形。

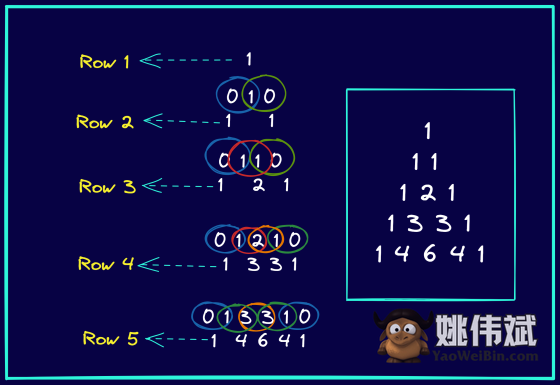
注意当你在某个数字上方只有一个数字时，你可以填充零。

📝作为一个快速的练习，按照上述步骤构造n = 6和n = 7的帕斯卡三角形。

接下来，让我们开始编写一些代码。你可以选择在浏览器中从Geekflare’s Python IDE上运行代码片段-当你阅读本教程时。

打印帕斯卡三角形的Python函数

在本节中，让我们编写一个Python函数来打印任意给定行数的帕斯卡三角形。

有两个关键问题需要考虑：

如何表示帕斯卡三角形中的元素？
如何打印带有适当间距和格式的帕斯卡三角形？

现在让我们来回答这些问题。

#1. 帕斯卡三角形中每个元素的表达式是什么？

碰巧帕斯卡三角形中的元素可以使用nCr的公式来获得。如果你还记得你在学校学过的数学，nCr表示从n个元素的集合中选择r个元素的方式数。

nCr的公式如下：

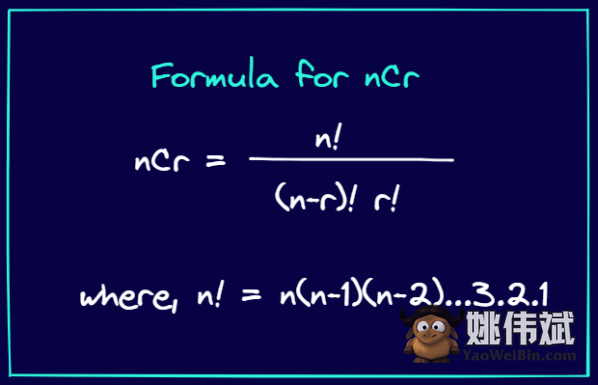
现在让我们使用nCr公式来表达帕斯卡三角形中的元素。

我们现在找到了一种表示矩阵中元素的方法。

#2. 打印模式时如何调整间距？

在帕斯卡三角形中，第numRows行有numRows - i个空格。你可以使用Python的range函数与for循环结合使用来实现这一点。

由于range函数默认排除终点，所以确保添加+ 1以获得所需的前导空格数。

现在你已经学会了如何表示元素，并在打印帕斯卡三角形时调整空格，让我们继续定义函数pascal_tri。

解析函数定义

那么你希望函数pascal_tri做什么？

函数pascal_tri应该接受行数(numRows)作为参数。
它应该打印帕斯卡三角形，行数为numRows。

为了计算阶乘，让我们使用Python的内置math模块中的factorial函数。

▶️ 运行下面的代码单元格来导入factorial并在当前模块中使用它。

from math import factorial

下面的代码片段包含了函数定义。

def pascal_tri(numRows):
  '''打印帕斯卡三角形'''
  for i in range(numRows):
    # 循环获取前导空格
	  for j in range(numRows-i+1):
		  print(end=" ")
    
    # 循环获取第i行的元素
	  for j in range(i+1):
		  # nCr = n!/((n-r)!*r!)
		  print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

	 # 在新行中打印每一行
	  print("n")

该函数的工作原理如下：

函数pascal_tri有一个必需的参数numRows：行数。
总共有numRows行。对于每一行，我们在第一项前添加numRows - i个前导空格。

然后，我们使用nCr公式计算各个项。对于第行，项为，其中j = {0,1,2,..,i}。

请注意，我们使用//进行整数除法，因为我们希望项是整数。

在计算完一行中的所有项后，以新行的形式打印下一行。

🔗 因为我们添加了一个docstring，所以您可以使用Python的内置help函数或__doc__属性来访问函数的文档字符串。下面的代码片段显示了如何做到这一点。

help(pascal_tri) # 输出 Help on function pascal_tri in module __main__: pascal_tri(numRows) 打印帕斯卡三角形 pascal_tri.__doc__ # 输出打印帕斯卡三角形。

现在让我们使用行数作为参数调用函数。

pascal_tri(3) # 输出 1 1 1 1 2 1

打印了帕斯卡三角形的前3行，和预期一样。

使用递归打印帕斯卡三角形

在前面的部分中，我们确定了帕斯卡三角形中每个项的数学表达式。然而，我们没有利用两个相邻行之间的关系。

实际上，我们使用前一行来计算后一行的项。我们不能利用这个关系来编写一个递归实现的pascal_tri函数吗？

是的，让我们来实现一下！

在递归实现中，一个函数重复调用自身，直到满足基本情况为止。在构造帕斯卡三角形时，我们从只有一个项1的第一行开始，然后构建后续行。

因此，函数调用pascal_tri(numRows)依次调用pascal_tri(numRows-1)，依此类推，直到达到基本情况pascal_tri(1)。

考虑需要打印帕斯卡三角形的前3行的示例。下面的图像说明了递归调用如何被推送到堆栈中。以及递归函数调用如何返回帕斯卡三角形的行。

在递归调用期间的调用堆栈（作者提供的图像）

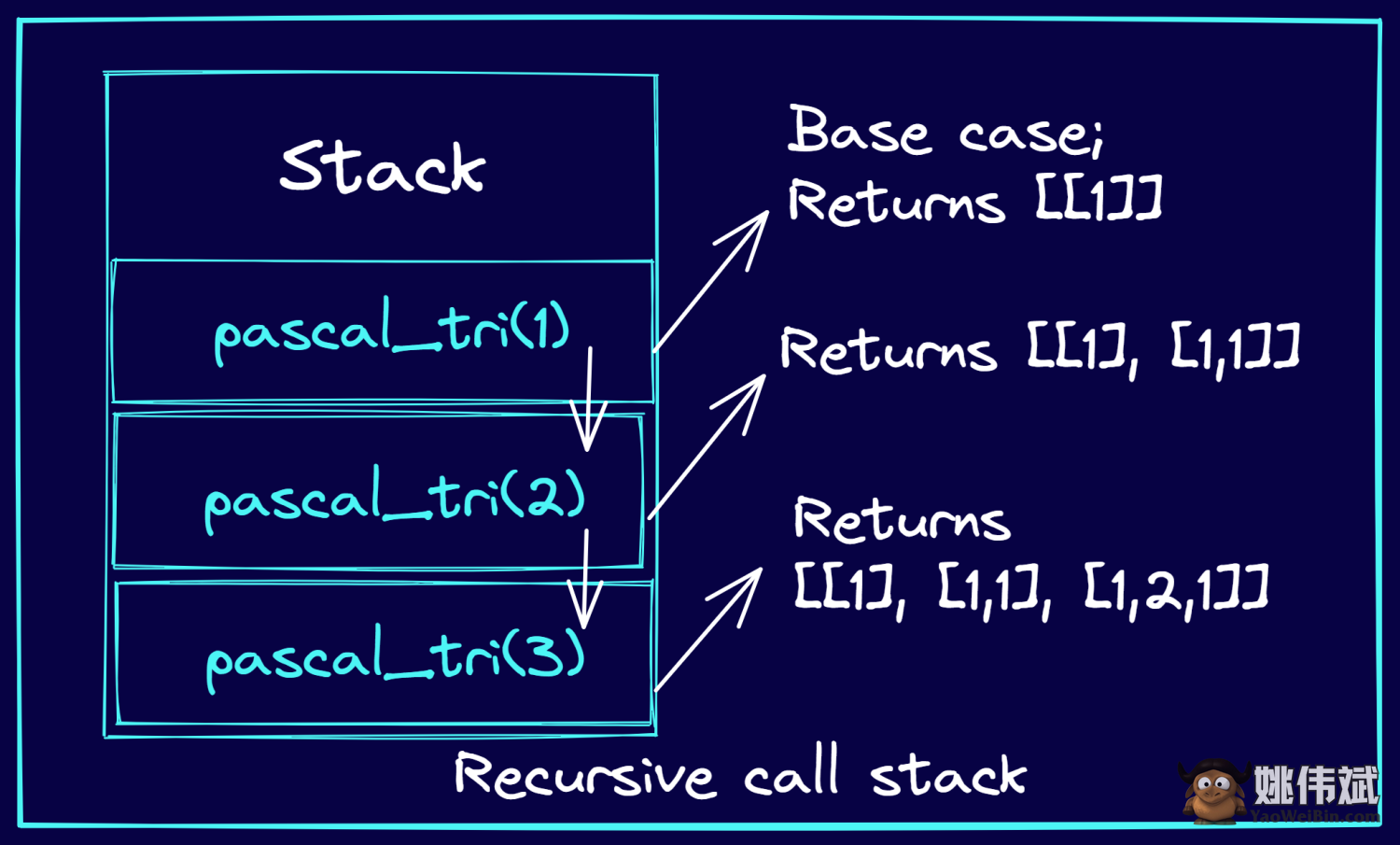
▶️ 运行下面的代码片段以递归生成帕斯卡三角形的行。

def pascal_tri(numRows): '''打印帕斯卡三角形''' if numRows == 1: return [[1]] # 达到基本情况！ else: res_arr = pascal_tri(numRows-1) # 递归调用pascal_tri # 使用前一行计算当前行 cur_row = [1] # 每一行都以1开始 prev_row = res_arr[-1] for i in range(len(prev_row)-1): # 上面2个项的总和 cur_row.append(prev_row[i] + prev_row[i+1]) cur_row += [1] # 每一行都以1结束 res_arr.append(cur_row) return res_arr

以下是值得注意的几点：

我们使用嵌套列表作为数据结构，其中帕斯卡三角的每一行都是一个列表，如下所示：[[第一行], [第二行], …，[第n行]]。

函数调用pascal_tri(numRows)触发了一系列递归调用，其中numRows - 1，numRows - 2一直到1作为参数。这些调用被推入堆栈。

当numRows == 1时，我们达到了基本情况，并且函数返回[[1]]。

现在返回的列表由调用堆栈中的后续函数使用，用于计算下一行。

如果cur_row是当前行，则cur_row[i] = prev_row[i] + prev_row[i+1]，即当前索引上方两个元素的和。

由于返回的数组是嵌套列表（列表的列表），我们需要调整间距并打印出条目，如下面的代码单元格所示。

tri_array = pascal_tri(5) for i,row in enumerate(tri_array): for j in range(len(tri_array) - i + 1): print(end=" ") # leading spaces for j in row: print(j, end=" ") # print entries print("n") # print new line

输出是正确的，如下所示！

# 输出 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1

打印帕斯卡三角形的Python函数，对于numRows ≤ 5

您学到的这两种方法都适用于打印任意行数numRows的帕斯卡三角形。

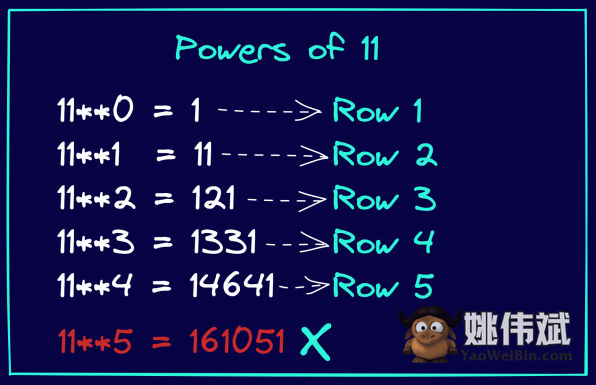
然而，有时您需要打印一个较小行数的帕斯卡三角形。当您需要打印的行数最多为5行时，可以使用一种直接的技术。

查看下面的图形。观察如何11的幂等于帕斯卡三角形中的条目。还要注意，这仅适用于11的4次幂。也就是说，11的幂次{0、1、2、3、4}给出了帕斯卡三角形的1到5行的条目。

让我们重写函数定义，如下所示：

def pascal_tri(numRows): '''打印numRows个帕斯卡三角形。''' for i in range(numRows): print(' '*(numRows-i), end='') # 计算11的幂 print(' '.join(str(11**i)))

函数pascal_tri的工作方式如下：

与之前的示例一样，我们调整间距。

然后，我们使用Python的乘方运算符（**）计算11的幂。

由于11的幂默认为整数，使用str()将其转换为字符串。现在将11的幂作为字符串。

Python中的字符串是可迭代的，因此您可以循环遍历它们并逐个访问一个字符。

接下来，您可以使用join()方法，语法为：.join()，使用作为分隔符加入中的元素。

这里，您需要字符之间的一个空格，因此将为' '，是字符串：11的幂。

让我们检查函数是否按预期工作。

pascal_tri(5) # 输出 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1

作为另一个例子，将数字4作为参数调用函数pascal_tri。

pascal_tri(4) # 输出 1 1 1 1 2 1 1 3 3 1

我希望您现在知道如何轻松打印1到5范围内的numRows的帕斯卡三角形。

结论

这是我们学到的内容：

如何使用给定的行数构造Pascal三角形。每一行的每个数字都是直接位于它上方的两个数字的和。

编写一个使用公式nCr = n!/(n-r)!.r!计算Pascal三角形条目的Python函数。

然后你学习了一个递归实现的函数。

最后，你学习了构造Pascal三角形的最优方法，对于numRows高达5，使用11的幂。

如果你想提升Python技能，学会使用 multiply matrices，检查一个number is prime，并解决problems on string operations。愉快编码！

相关