3种在Python中矩阵相乘的方法
在本教程中，您将学习如何在Python中矩阵相乘。
您将首先学习有效矩阵乘法的条件，并编写一个自定义的Python函数来进行矩阵乘法。接下来，您将看到如何使用嵌套列表推导式实现相同的结果。
最后，您将使用NumPy及其内置函数来更高效地执行矩阵乘法。
如何检查矩阵乘法是否有效
在编写矩阵乘法的Python代码之前，让我们重新回顾一下矩阵乘法的基础知识。
只有当矩阵A的列数等于矩阵B的行数时，矩阵A和B之间的矩阵乘法才有效。
您可能以前已经遇到过这个矩阵乘法的条件。但是，您是否想过为什么会这样呢？
嗯，这是因为矩阵乘法的工作方式。看看下面的图片。
在我们的通用示例中，矩阵A有m行和n列。矩阵B有n行和p列。
结果矩阵的形状是什么？
结果矩阵C中索引(i, j)处的元素是矩阵A的第i行与矩阵B的第j列的点积。
因此，要获取结果矩阵C中特定索引处的元素，您需要分别计算矩阵A和B的相应行和列的点积。
重复上面的过程，您将得到形状为m x p的乘积矩阵C，其中m行p列，如下所示。
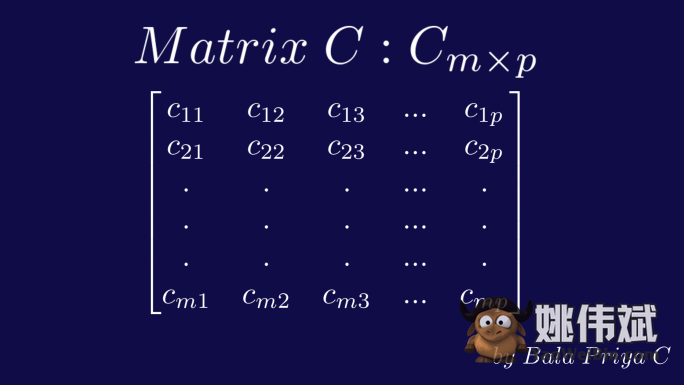
而两个向量a和b之间的点积或内积由以下方程给出。
现在让我们总结一下：
- 很明显，点积仅在长度相等的向量之间被定义。
- 因此，在乘法两个矩阵时，为了使行和列之间的点积有效，您需要它们具有相同数量的元素。
- 在上面的通用示例中，矩阵A中的每一行都有n个元素。矩阵B中的每一列也有n个元素。
如果仔细观察一下，n是矩阵A的列数，也是矩阵B的行数。这正是您需要矩阵A的列数等于矩阵B的行数的原因。
我希望您能理解矩阵乘法有效的条件以及如何获得乘积矩阵中的每个元素。
让我们继续编写一些Python代码来相乘两个矩阵。
编写一个自定义的Python函数来相乘矩阵
作为第一步，我们编写一个自定义函数来相乘矩阵。
该函数应该执行以下操作：
- 将矩阵A和B作为输入接受。
- 检查矩阵A和B之间的矩阵乘法是否有效。
- 如果有效，则相乘矩阵A和B，并返回乘积矩阵C。
- 否则，返回一个错误消息，说明矩阵A和B不能相乘。
步骤1：使用NumPy的random.randint()函数生成两个整数矩阵。您也可以将矩阵声明为嵌套的Python列表。
导入numpy库并设置种子为27。
将A和B定义为3×3和3×2的随机整数矩阵。
输出矩阵A和B。
定义一个函数multiply_matrix(A，B)，该函数接受两个矩阵A和B作为输入，并返回乘积矩阵C（如果矩阵乘法有效）。
在函数中，首先将C声明为全局变量，然后使用shape属性检查A和B是否可以相乘。如果可以相乘，就创建一个全零矩阵C，并使用嵌套循环计算C的每个元素的值。
最后，调用multiply_matrix函数并打印输出结果。
给定矩阵A的第i行和矩阵B的第j列，下面的表达式给出矩阵C中索引（i，j）处的元素。
sum(a*b for a,b in zip(A_row, B_col)
# zip(A_row, B_col)返回一个元组的迭代器
# 如果A_row = [a1, a2, a3] 和 B_col = [b1, b2, b3]
# zip(A_row, B_col)返回(a1, b1), (a2, b2)等如果 i = j = 1，该表达式将返回矩阵C的第c_11个元素。因此，您可以通过这种方式获取一行中的一个元素。
步骤2：构建矩阵C中的一行
我们的下一个目标是构建一个完整的行。
对于矩阵A中的第1行，您需要遍历矩阵B中的所有列以获取矩阵C中的一行。
回到列表推导模板。
- 将
替换为第1步中的表达式，因为这是您想要做的。 - 接下来，将
替换为B_col，即矩阵B中的每一列。 - 最后，将
替换为zip(*B)，即包含矩阵B中所有列的列表。
下面是第一个列表推导式。
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
# zip(*B)：*是解压操作符
# zip(*B)返回矩阵B中的列的列表Step 3: 构建所有行并获取矩阵C
接下来，您需要通过计算其余的行来填充乘积矩阵C。
为此，您需要遍历矩阵A中的所有行。
再次回到列表推导式，并执行以下操作。
- 将
替换为第2步中的列表推导式。回想一下，我们在前一步计算了一整行。 - 现在，将
替换为A_row，即矩阵A中的每一行。 - 您的
是矩阵A本身，因为您正在遍历其行。
这是我们最终的嵌套列表推导式。🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]是时候验证结果了！✔
# 使用np.array()转换为NumPy array
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# 输出：
[[ 89 107]
[ 47 49]
[ 40 44]]如果您仔细观察，可以看到这与我们之前的嵌套循环完全相同，只是更加简洁。
您还可以使用一些内置函数更加高效地完成所有这些操作。让我们在下一节学习这些函数。
使用NumPy的matmul()函数在Python中进行矩阵乘法
np.matmul()函数接受两个矩阵作为输入，并返回矩阵乘法的结果，如果输入矩阵的乘法是有效的。
C = np.matmul(A,B)
print(C)
# 输出：
[[ 89 107]
[ 47 49]
[ 40 44]]注意，这种方法比我们之前学到的两种方法更简单。实际上，除了使用np.matmul()，您还可以使用等效的@运算符，我们将立即看到。
如何使用@运算符在Python中进行矩阵乘法
在Python中，@是用于矩阵乘法的二元运算符。
它对两个矩阵（通常是N维NumPy数组）进行操作，并返回乘积矩阵。
注意：您需要使用Python 3.5及更高版本才能使用
@运算符。
以下是您可以使用它的方式。
C = A@B
print(C)
# 输出
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])注意，乘积矩阵C与我们之前获得的结果相同。
您可以使用np.dot()函数进行矩阵乘法吗？
如果您曾经遇到过使用np.dot()来计算两个矩阵的乘法的代码，那么下面是它的工作方式。
C = np.dot(A,B)
print(C)
# 输出结果:
[[ 89 107]
[ 47 49]
[ 40 44]]您会发现np.dot(A, B)也返回了预期的乘积矩阵。
然而，根据NumPy docs，您应该只使用np.dot()来计算两个一维向量的点积，而不是矩阵乘法。
从前一节中可以看出，乘积矩阵C中索引（i，j）处的元素是矩阵A的第i行和矩阵B的第j列的点积。
由于NumPy将此点积操作隐式地广播到所有行和所有列，因此您可以得到结果乘积矩阵。但为了使代码可读且避免歧义，请改用np.matmul()或@运算符。
结论
🎯 在本教程中，您学到了以下内容。
- 矩阵乘法有效的条件：矩阵A的列数等于矩阵B的行数。
- 如何编写一个自定义的Python函数来检查矩阵乘法是否有效，并返回乘积矩阵。函数的主体使用嵌套的for循环。
- 接下来，您学习了如何使用嵌套的列表推导式来乘法矩阵。它们比for循环更简洁，但容易出现可读性问题。
- 最后，您学习了如何使用NumPy内置函数np.matmul()来乘法矩阵，以及在速度方面这是最高效的。
- 您还学习了如何使用Python中的@运算符来乘法两个矩阵。
这就结束了我们关于Python矩阵乘法的讨论。作为下一步，学习如何检查一个number is prime in Python。或者解决有趣的problems on Python strings。
祝学习愉快！🎉
